数的节点代表集合,根代表关系
树-广度优先遍历(层序遍历)
树-深度优先遍历(深度遍历)
用于判断父子节点关系
二叉树
1、每个节点度最多为2
2、度为0的节点比度为2的节点多1个:$n_0$+$n_1$+$n_2$=$n_1$+2$n_2$+1
完全二叉树,满二叉树,完美二叉树
完全二叉树 (complete binary tree)
1、编号为 i 的子节点:
- 左孩子编号:2i
- 右孩子编号:2i+1
2、可以用连续空间存储(数组)
通过计算而非记录得到子节点地址,节省空间
左孩子右兄弟表示法节省空间
二叉树代码演示
struct Node {
int key;
Node *lchild, *rchild;
Node(int key) : key(key), lchild(NULL), rchild(NULL) {}
};
Node* getNewNode(int key) {
return new Node(key);
}
Node* insert(Node* root, int key) {
if (root == NULL) return getNewNode(key);
if (rand() % 2) root->lchild = insert(root->lchild, key);
else root->rchild = insert(root->rchild, key);
return root;
}
void clear(Node* root) {
if (root == NULL) return;
clear(root->lchild);
clear(root->rchild);
delete root;
}
void bfs(Node* root) {//广度优先遍历
if (root == NULL) return;
queue<Node*> q;
q.push(root);
while (!q.empty()) {
Node* node = q.front();
q.pop();
cout << "\nnode : " << node->key << "\n";
if (node->lchild) {
q.push(node->lchild);
cout <<"\t"<< node->key <<"->"<< node->lchild->key <<"(left)\n";
}
if (node->rchild) {
q.push(node->rchild);
cout <<"\t"<< node->key <<"->"<< node->rchild->key <<"(right)\n";
}
}
}
int tot = 0;
void dfs(Node* root) {//深度优先遍历
if (root == NULL) return;
int start, end;
tot += 1;
start = tot;
if (root->lchild) dfs(root->lchild);
if (root->rchild) dfs(root->rchild);
tot += 1;
end = tot;
cout << root->key << " : [" << start << ", " << end << "]\n";
}用其中两种遍历(必须含中序遍历)就可以恢复二叉树
class Node {
public:
int key;
int ltag, rtag; // 1 : thread, 0 : edge
Node *lchild, *rchild;
Node(int key) : key(key), ltag(0), rtag(0), lchild(nullptr), rchild(nullptr) {}
};
class ThreadedBinaryTree {
public:
Node *root;
Node *pre_node;
Node *inorder_root;
ThreadedBinaryTree():root(nullptr),pre_node(nullptr),inorder_root(nullptr) {}
Node* insert(Node *root, int key) {
if (root == nullptr) return new Node(key);
if (rand() % 2) root->lchild = insert(root->lchild, key);
else root->rchild = insert(root->rchild, key);
return root;
}
void clear(Node *root) {
if (root == nullptr) return;
if (root->ltag == 0) clear(root->lchild);
if (root->rtag == 0) clear(root->rchild);
delete root;
}
void pre_order(Node *root) const {
if (root == nullptr) return;
cout << root->key << " ";
if (root->ltag == 0) pre_order(root->lchild);
if (root->rtag == 0) pre_order(root->rchild);
}
void in_order(Node *root) const {
if (root == nullptr) return;
if (root->ltag == 0) in_order(root->lchild);
cout << root->key << " ";
if (root->rtag == 0) in_order(root->rchild);
}
void post_order(Node *root) const {
if (root == nullptr) return;
if (root->ltag == 0) post_order(root->lchild);
if (root->rtag == 0) post_order(root->rchild);
cout << root->key << " ";
}
void __build_inorder_thread(Node *root) {
if (root == nullptr) return;
if (root->ltag == 0) __build_inorder_thread(root->lchild);
if (inorder_root == nullptr) inorder_root = root;
if (root->lchild == nullptr) {
root->lchild = pre_node;
root->ltag = 1;
}
if (pre_node && pre_node->rchild == nullptr) {
pre_node->rchild = root;
pre_node->rtag = 1;
}
pre_node = root;
if (root->rtag == 0) __build_inorder_thread(root->rchild);
}
void build_inorder_thread(Node *root) {
__build_inorder_thread(root);
if (pre_node) {
pre_node->rchild = nullptr;
pre_node->rtag = 1;
}
}
Node* getNext(Node *root) {
if (root->rtag == 1) return root->rchild;
root = root->rchild;
while (root->ltag == 0 && root->lchild) root = root->lchild;
return root;
}
};二叉树的广义表表示法
class Node {
public:
int key;
Node *lchild, *rchild;
Node(int key) : key(key), lchild(nullptr), rchild(nullptr) {}
};
Node* insert(Node* root, int key) {
if (root == nullptr) return new Node(key);
if (rand() % 2) root->lchild = insert(root->lchild, key);
else root->rchild = insert(root->rchild, key);
return root;
}
Node* getRandomBinaryTree(int n) {
Node* root = nullptr;
for (int i = 0; i < n; i++) {
root = insert(root, rand() % 100);
}
return root;
}
void clear(Node* root) {
if (root == nullptr) return;
clear(root->lchild);
clear(root->rchild);
delete root;
}
string buff;
int len = 0;
void __serialize(Node* root) {//二叉树转广义表
if (root == nullptr) return;
buff += to_string(root->key);
if (root->lchild == nullptr && root->rchild == nullptr) return;
buff += "(";
__serialize(root->lchild);
if (root->rchild) {
buff += ",";
__serialize(root->rchild);
}
buff += ")";
}
string serialize(Node* root) {
buff.clear();
len = 0;
__serialize(root);
return buff;
}
void print(Node* node) {
if (node == nullptr) return;
cout << node->key << "("
<< (node->lchild ? node->lchild->key : -1) << ", "
<< (node->rchild ? node->rchild->key : -1) << ")\n";
}
void output(Node* root) {
if (root == nullptr) return;
print(root);
output(root->lchild);
output(root->rchild);
}
Node* deserialize(const string& buff) {//广义表转二叉树,利用栈
stack<Node*> s;
int flag = 0, scode = 0;
Node* p = nullptr, * root = nullptr;
for (size_t i = 0; i < buff.size(); i++) {
switch (scode) {
case 0: {
if (buff[i] >= '0' && buff[i] <= '9') scode = 1;
else if (buff[i] == '(') scode = 2;
else if (buff[i] == ',') scode = 3;
else scode = 4;
i -= 1;
} break;
case 1: {
int key = 0;
while (i < buff.size() && buff[i] >= '0' && buff[i] <= '9') {
key = key * 10 + (buff[i] - '0');
i += 1;
}
p = new Node(key);
if (!s.empty() && flag == 0) s.top()->lchild = p;
if (!s.empty() && flag == 1) s.top()->rchild = p;
i -= 1;
scode = 0;
} break;
case 2: {
s.push(p);
flag = 0;
scode = 0;
} break;
case 3: {
flag = 1;
scode = 0;
} break;
case 4: {
root = s.top();
s.pop();
scode = 0;
} break;
}
}
return root;
}
int main() {
Node* root = getRandomBinaryTree(10);
string serialized = serialize(root);
cout << "Serialized: " << serialized << endl;
Node* deserializedRoot = deserialize(serialized);
output(deserializedRoot);
clear(root);
clear(deserializedRoot);
return 0;
}最优变长编码:哈夫曼编码
定长编码vs变长编码
哈夫曼编码生成过程:
1.首先,统计得到每一种字符的概率
2.每次将最低频率的两个节点合并成一棵子树
3.经过了 n-1 轮合并,就得到了一棵哈夫曼树
4.按照左0,右1的形式,将编码读取出来
结论:哈弗曼编码,是最优的变长编码
证明
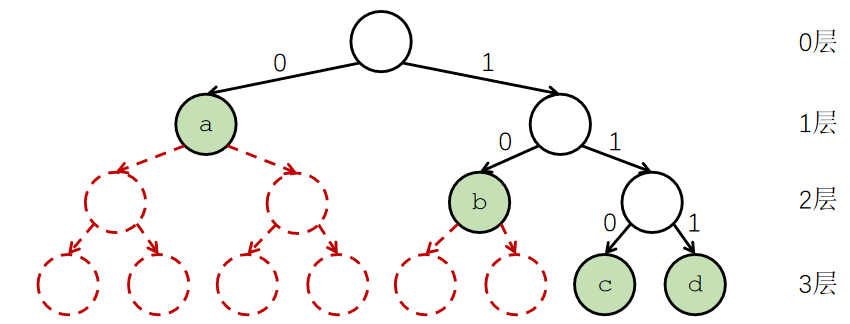
$设总共H层,则第H层共有2^H个节点,设第i个字符处于Li层,则其覆盖第H层2^{H-Li}个节点$
$2^{H−L_1} + 2^{H−L_2} + 2^{H−L_3} + \dots + 2^{H−L_n} \leq 2^H$
$同时除以2^H$
$\frac{1}{2^{L_1}} + \frac{1}{2^{L_2}} + \frac{1}{2^{L_3}} + \dots + \frac{1}{2^{L_n}} \leq 1$
$设 L'_i = −L_i$, $得到: 2^{L'_1} + 2^{L'_2} + \dots + 2^{L'_n} \leq 1$
$所以得证明公式的约束条件: \sum 2^{L_i} \leq 1$
$证明:\sum p_i \times l_i最小$
$又因为L'_i = −L_i,所以等价于 −\sum p_i \times L'_i$
$在设 I_i = 2^{L_i} \Rightarrow L'_i = \log_2 I_i \Rightarrow −\sum p_i \times \log_2 I_i$
$让这个式子达到最小值$
$同时得到:约束 \sum I_i \leq 1$
$目标: -\sum p_i \times \log_2 I_i 达到最小值$
$目标函数展开: -\left(P_1 \log_2 I_1 + P_2 \log_2 I_2 + \dots + P_n \log_2 I_n\right)$
$约束条件为: \sum I_i \leq 1$
$证明当目标函数达到最小值的时候, 想看看什么情况下目标函数能达到最优解, 让他最小$
$是不是需要让括号里面尽可能大, 需要让 \sum I_i = 1$
$我们采用反证: 如果 \sum I_i < 1的时候目标函数有最小的解$
$那么 I_1 + I_2 + I_3 + \dots + I_n < 1, 但是我们可以让它变成 = 1$
$I_1 + I_2 + I_3 + \dots + I_n + I'_x = 1整个式子多了一个I'_x, 并且是大于0的值$
$将 I'_x加到目标函数−(P_1 \log_2 I_1 + P_2 \log_2 I_2 + \dots + P_n \log_2 I_n)里面$
$括号里面的内容变的更大了, 那么整体就变的更小了$
$所以得到 \sum I_i = 1$
$继续证明$
$目标函数: -\left(P_1 \log_2 I_1 + P_2 \log_2 I_2 + \dots + P_n \log_2 I_n\right)$
$当目标函数达到条件: I_1 + I_2 + I_3 + \dots + I_n = 1$
$设 I_n = 1 - II$
$目标函数变成: -\left(P_1 \log_2 I_1 + P_2 \log_2 I_2 + \dots + P_n \log_2 \left(1 - II\right)\right)$
$想让这个式子达到最小值, 对每一项求偏导, 让每一项偏导等于0$
$对 I_1 求偏导: \frac{P_1}{I_1 \ln 2} - \frac{P_n}{(1 - II)\ln 2} = 0$
$对 I_2 求偏导: \frac{P_2}{I_2 \ln 2} - \frac{P_n}{(1 - II)\ln 2} = 0$
$对 I_3 求偏导: \frac{P_3}{I_3 \ln 2} - \frac{P_n}{(1 - II)\ln 2} = 0$
$整理后得到: $
$\frac{P_1}{I_1} = \frac{P_2}{I_2} = \frac{P_3}{I_3} = \dots = \frac{P_n}{I_n}$
$P_i = I_i = 2^{l'_i} = \frac{1}{2^{l_i}}$
$l_i是编码长度,P_i是字符概率$
$得到结论,编码越大,概率越小$
代码
class Node {
public:
char ch;
int freq;
Node *lchild, *rchild;
Node(int freq, char ch) : ch(ch), freq(freq), lchild(nullptr), rchild(nullptr) {}
};
Node* getNewNode(int freq, char ch) {
return new Node(freq, ch);
}
void swap_node(vector<Node*>& node_arr, int i, int j) {
Node* temp = node_arr[i];
node_arr[i] = node_arr[j];
node_arr[j] = temp;
}
int find_min_node(const vector<Node*>& node_arr, int n) {
int ind = 0;
for (int j = 1; j <= n; j++) {
if (node_arr[ind]->freq > node_arr[j]->freq) ind = j;
}
return ind;
}
Node* buildHaffmanTree(vector<Node*>& node_arr) {
int n = node_arr.size();
for (int i = 1; i < n; i++) {
// Find two nodes with the smallest frequency,可以用堆和优先队列优化
int ind1 = find_min_node(node_arr, n - i);
swap_node(node_arr, ind1, n - i);
int ind2 = find_min_node(node_arr, n - i - 1);
swap_node(node_arr, ind2, n - i - 1);
// Merge two nodes
int freq = node_arr[n - i]->freq + node_arr[n - i - 1]->freq;
Node* node = getNewNode(freq, 0);
node->lchild = node_arr[n - i - 1];
node->rchild = node_arr[n - i];
node_arr[n - i - 1] = node;
}
return node_arr[0];
}
void clear(Node* root) {
if (root == nullptr) return;
clear(root->lchild);
clear(root->rchild);
delete root;
}
unordered_map<char, string> char_code;
void extractHaffmanCode(Node* root, string& buff, int k) {
if (root->lchild == nullptr && root->rchild == nullptr) {
char_code[root->ch] = buff;
return;
}
buff.push_back('0');
extractHaffmanCode(root->lchild, buff, k + 1);
buff.pop_back();
buff.push_back('1');
extractHaffmanCode(root->rchild, buff, k + 1);
buff.pop_back();
}Leetcode-589 N叉树的前序遍历
class Solution {
public:
void __preorder(Node* root, vector<int>& ans) {
if (root == NULL)
return;
ans.push_back(root->val);
for (auto x : root->children) {
__preorder(x, ans);
}
return;
}
vector<int> preorder(Node* root) {
vector<int> res;
__preorder(root,res);
return res;
}
};Leetcode-105 从前序与中序遍历序列构造二叉树
class Solution {
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
if (preorder.size() == 0) return NULL;
int pos = 0, n = preorder.size();
while (inorder[pos] != preorder[0]) pos += 1;
TreeNode *root = new TreeNode(preorder[0]);
vector<int> preArr, inArr;
for (int i = 1; i <= pos; i++) preArr.push_back(preorder[i]);
for (int i = 0; i < pos; i++) inArr.push_back(inorder[i]);
root->left = buildTree(preArr, inArr);
preArr.clear();
inArr.clear();
for (int i = pos + 1; i < n; i++) preArr.push_back(preorder[i]);
for (int i = pos + 1; i < n; i++) inArr.push_back(inorder[i]);
root->right = buildTree(preArr, inArr);
return root;
}
};Leetcode-102 二叉树的层序遍历
法一:队列
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
if (root == NULL) return vector<vector<int>>();
TreeNode *node;
queue<TreeNode *> q;
q.push(root);
vector<vector<int>> ans;
while (!q.empty()) {
int cnt = q.size();
vector<int> temp;
for (int i = 0; i < cnt; i++) {
node = q.front();
temp.push_back(node->val);
if (node->left) q.push(node->left);
if (node->right) q.push(node->right);
q.pop();
}
ans.push_back(temp);
}
return ans;
}
};法二:DFS
class Solution {
public:
void dfs(TreeNode *root, int k, vector<vector<int>> &ans) {
if (root == NULL) return ;
if (k == ans.size()) ans.push_back(vector<int>());
ans[k].push_back(root->val);
dfs(root->left, k + 1, ans);
dfs(root->right, k + 1, ans);
return ;
}
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> ans;
dfs(root, 0, ans);//ans是传出参数
return ans;
}
};Leetcode-226 翻转二叉树
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if (root == NULL) return NULL;
swap(root->left, root->right);
invertTree(root->left);
invertTree(root->right);
return root;
}
};Leetcode-107 二叉树的层序遍历Ⅱ
class Solution {
public:
void dfs(TreeNode *root, int k, vector<vector<int>> &ans) {
if (root == NULL) return ;
if (k == ans.size()) ans.push_back(vector<int>());
ans[k].push_back(root->val);
dfs(root->left, k + 1, ans);
dfs(root->right, k + 1, ans);
return ;
}
vector<vector<int>> levelOrderBottom(TreeNode* root) {
vector<vector<int>> ans;
dfs(root, 0, ans);
for (int i = 0, j = ans.size() - 1; i < j; i++, j--) {
swap(ans[i], ans[j]);
}
return ans;
}
};Leetcode–103 二叉树的锯齿形层序遍历
class Solution {
public:
void dfs(TreeNode *root, int k, vector<vector<int>> &ans) {
if (root == NULL) return ;
if (k == ans.size()) ans.push_back(vector<int>());
ans[k].push_back(root->val);
dfs(root->left, k + 1, ans);
dfs(root->right, k + 1, ans);
return ;
}
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
vector<vector<int>> ans;
dfs(root, 0, ans); // step1
// step2
for (int k = 1; k < ans.size(); k += 2) {
for (int i = 0, j = ans[k].size() - 1; i < j; i++, j--) {
swap(ans[k][i], ans[k][j]);
}
}
return ans;
}
};Leetcode-LCR143 子结构判断
class Solution {
public:
bool match_one(TreeNode *A, TreeNode *B) {
if (A == NULL) return B == NULL;
if (B == NULL) return true;
if (A->val != B->val) return false;
return match_one(A->left, B->left) && match_one(A->right, B->right);
}
bool isSubStructure(TreeNode* A, TreeNode* B) {
if (A == NULL) return B == NULL;
if (B == NULL) return false;
if (A->val == B->val && match_one(A, B)) return true;
if (isSubStructure(A->left, B)) return true;
if (isSubStructure(A->right, B)) return true;
return false;
}
};